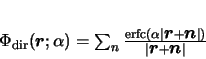Next: PME Equations
Up: Equations
Previous: Equations
Contents
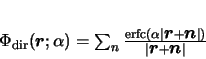 |
(2) |
erfc is the complementary error function:
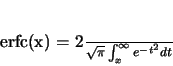 |
(3) |
(Computer implementation of erfc given in A.4.1: derfc.F)
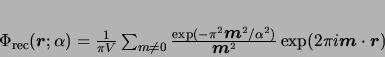 |
(4) |
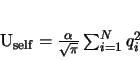 |
(5) |
In these equations, 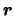 represents a distance between two particles8,
represents a distance between two particles8, 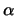 is a constant which can be adjusted to tweak the output values, and
is a constant which can be adjusted to tweak the output values, and 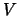 is the volume of the unit cell we are looking at. As mentioned under our description of the PME method, we replicate a particular region many times to create a realistic biological system. This is the volume of one such region.
is the volume of the unit cell we are looking at. As mentioned under our description of the PME method, we replicate a particular region many times to create a realistic biological system. This is the volume of one such region. 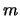 and
and 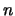 are just unit vectors9 normal faces of the unit cell.
The self-interaction term, see Appendix A.3: selfTerm.F for code, is a relatively simple function that simply corrects for the fact that the other terms calculate a particle's potential relative to its own charge field, which must be accounted for.
The real space term, see Appendix A.4: realTerm.F for code, calculates short range interactions. It makes use of a cutoff radius to limit computational cost. Because this term is short range, the contributions to it from distant particles are very small, and neglecting them does not significantly impair accuracy. Because computing the interactions from all particles would make this term
are just unit vectors9 normal faces of the unit cell.
The self-interaction term, see Appendix A.3: selfTerm.F for code, is a relatively simple function that simply corrects for the fact that the other terms calculate a particle's potential relative to its own charge field, which must be accounted for.
The real space term, see Appendix A.4: realTerm.F for code, calculates short range interactions. It makes use of a cutoff radius to limit computational cost. Because this term is short range, the contributions to it from distant particles are very small, and neglecting them does not significantly impair accuracy. Because computing the interactions from all particles would make this term
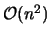 which would make it the slowest portion of the code, the cutoff radius is very important. To implement the cutoff radius we make use of integer rounding and division to rapidly compute which particles are within a certain radius of a given particle, and the calculate their effects on the given particle. Because the number of particles that must be calculated for each particle is
which would make it the slowest portion of the code, the cutoff radius is very important. To implement the cutoff radius we make use of integer rounding and division to rapidly compute which particles are within a certain radius of a given particle, and the calculate their effects on the given particle. Because the number of particles that must be calculated for each particle is
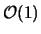 , this allows the real space term to be
, this allows the real space term to be 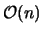 .
.
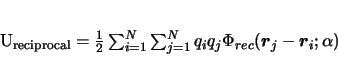 |
(6) |
10.
In this, 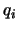 and
and 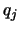 are charges of particles in the system and
are charges of particles in the system and 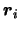 and
and 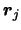 refer to the respective positions of these charges.
refer to the respective positions of these charges. 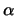 and
and 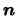 are the same as referred to in the previous equation.
are the same as referred to in the previous equation.




Next: PME Equations
Up: Equations
Previous: Equations
Contents
Thomas G Dimiduk
2004-04-15