



Next: Cardinal B-Splines
Up: Results
Previous: Results
Contents
We have written code that computes the complementary error function (erfc) accurately to the limits of a double precision real variable. The error function is an integral that cannot be solved analytically, see equation 3, for all of the cases we need, so we have used a rational Chebyshev expansion13 to rapidly approximate the erfc to the required accuracy. Our mentor has code that computed the error function, but it has several problems, one of them fairly severe. The first problem was that her code was not as accurate as is needed. The second, more troublesome problem was that her program that used the error function gave different results when ran on IBM AIX and Linux machines. To correct this we found and wrote several functions to approximate the error function and tested them on both machines. Eventually we found that we were encountering a namespace conflict, the IBM complier had an intrinsic function to evaluate error functions and it was calling that function automatically. We then ran comparisons of the outputs of five different error function implementations: our mentor's original code, our corrected version of that code, the intrinsic function in the IBM xlf90 compiler, code the naval surface warfare group make available, and a function we wrote. Our function, the IBM function, and the naval surface warfare codes all gave correct results out to the limit of accuracy we compared. We decided to use the naval surface warfare code (code in Appendix A.4.1) because the IBM code was only usable on that compiler, and we assume that their code has been more completely checked than ours. We also have reason to believe that the naval surface warfare code may be more accurate than our code. They stated that it was accurate to 14 decimal places [23], while we are only sure of ours to 12 decimal places.
Figure 1:
Output of derfc.F for
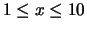
![\includegraphics[scale=0.7]{erfc.eps}](img41.png) |




Next: Cardinal B-Splines
Up: Results
Previous: Results
Contents
Thomas G Dimiduk
2004-04-15
![\includegraphics[scale=0.7]{erfc.eps}](img41.png)