The first step in creating our simulation was to convert our scientific knowledge of neural structures into a numerical model, that is easily translated into a computer program. We took information about the structures of neurons, the amount of stimuli each neuron requires to fire, the way each neuron is connected to other neurons, and the time required for a neuron to recover after it has fired. Using experimental data and graphs we assigned each variable a numerical value; this gave us a numerical model of the neuron interactions.

Next, we adapted our numerical model to a program that builds a matrix of neurons that are linked together. Then the program calculates the values of each neuron at a given time, stores that data in a file, and repeats the process based on the new information. We wrote another program to convert all the numerical values in the original file into xpm or ppm graphics files. This also converts each set of values into a frame of animation. These graphics files are then assembled into an MPEG video by a program called MPEG Encode.

Please refer toAppendix A for the source code to our program.

The details of the program begin with the fact that it contains a structure, which groups all the information that is needed for the entire program together, called “brain.” This structure contains variables such the width and the height of the matrix of neurons, total number of neurons, how neurons are linked together, and the values of every neuron for the current and proceeding frames. Using a structure allows us to easily add variables to the structure as the computations become more complex.

All the information that does not change, after the program first assembles the matrix, is stored in a "static" array within the structure. Information that is constantly changing is stored in two "dynamic" arrays, one for the current frame, and one for the next frame. Once the computer has completed the computation of the next frame based on the current frame it swaps the two dynamic structures. The information for the current frame is no longer needed so the program uses the information that was the next frame as the current frame and repeats the computations. We employed this method of having two dynamic arrays because it allows for excellent parallelization of the computations.

(Figure P.1- An illustration of the idea of successive serial and parallel regions.)

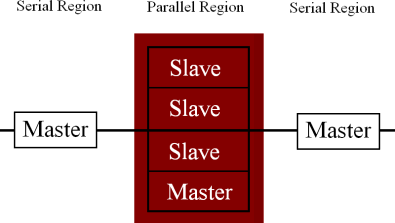
Because we planned to run our program on a parallel processing supercomputer it was essential that the program parallelized well. However, not every portion of the program is capable of running on multiple processors. For every execution the program must initialize the static information, and between each frame the program must write its data to a file. This causes a cycle of serial and parallel regions. In order to tell the compiler which sections were parallel and which were serial, we inserted compiler directives called pragmas into our code. To run on multiple processors the program splits into several simultaneously running programs called threads. A master thread executes the serial regions, writing output, and initializing, and the slave threads divide the work in parallel regions among themselves. During the serial periods, the slave threads must wait in a process called spin locking. Although spin locking actually decreases the wall clock time, or actual time the program took to execute, it consumes an enormous amount of CPU time. As more processors are added, the parallel regions take less time because each processor has a smaller amount of computations to complete. Each serial region always takes the same amount of time, so as processors are added each processor spends a greater percentage of its time waiting, or spin locking. We ran many tests that confirmed this hypothesis.