



Next: PME
Up: Specific problem
Previous: Solution Strategy
Contents
The first large problem we encounter in trying to calculate the electrostatic interactions is that to find the value we would have to evaluate an infinite conditionally convergent sum. However, the implementation of a periodic system also allows us to employ the Ewald method, which is specifically designed for computing electrostatic interactions in periodic systems. Ewald summation allows us to convert the conditionally convergent sum into two rapidly convergent sums [18] [10]. This splits the sum into two portions, one of which is evaluated in real (direct) space and one in reciprocal (Fourier) space5. The Ewald sum works by neutralizing long range forces with the introduction of a Gaussian cloud of opposite charge around the particle in question.6 The portion of the charges not masked by the Gaussians comprises the real space term. The Fourier space reciprocal space term removes the contribution of the Gaussians, giving the same value as the original sum. Without the Ewald method, it would be impossible to model the system because even forces far outside the scope of the model would need to be included. The problem with The Ewald technique is that to compute the reciprocal space term, we have to compute a Fourier transform, which is very slow relative to the rest of our program,
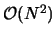




Next: PME
Up: Specific problem
Previous: Solution Strategy
Contents
Thomas G Dimiduk
2004-04-15