Computing Ewald Energy

Our most significant accomplishment has been writing a subroutine that calculates the Coulombic potential energy of a lattice of atoms using the Particle Mesh Ewald technique. As discussed earlier, this consists of three terms that add together to give the total electrostatic energy. Our code for the functions is in Appendices selfTerm.F, realTerm.F and recpTerm.F, computing, respectively, the self-interaction correction, the real space interactions, and the reciprocal space interactions. The real space term uses the erfc approximation function to perform the most difficult portion of the math, and a cutoff radius to reduce the computation to 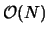$\mathcal{O}(N)$. The reciprocal space term uses the Cardinal B-Spline functions to construct a discrete mesh that approximates the charge distribution of the particle lattice. A series of loops and if statements allow us to interpolate a charge mesh from the particles with varying degrees of accuracy. We have currently implemented interpolation for Cardinal B-Splines of order two through six. We then make use of fast Fourier transforms from the FFTW library [21] to perform the required transform to reciprocal space. Our code starts with a file, lattice.dat (see Appendix B), that describes the geometry of a system of particles. We have succeeded in producing results that compare well to the conventional Ewald code we used for comparison. As demonstrated in Appendices C.2 and C.1, our code produces results that agree with the standard, Conventional Ewald, to within three significant figures. We hope by the final presentation to test our code on more and larger lattices and run timing studies comparing our code to the conventional Ewald code.